Using this table for Z Transforms with Discrete Indices
Shortened 2-page pdf of Laplace Transforms and Properties
Shortened 2-page pdf of Z Transforms and Properties
All time domain functions are implicitly=0 for t<0 (i.e. they are multiplied by unit step).
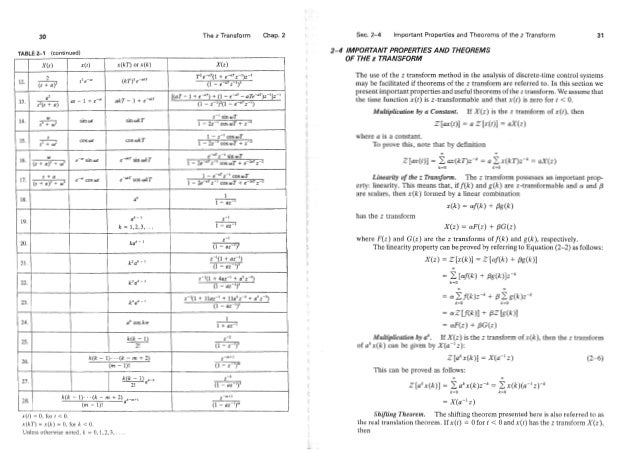
Table 2: Some common z Transforms. 2.3 Characteristic Polynomial. The derivation leading up to (21) points up a very important and useful property of the z transform: All of the elements in the response of the system to an input come from the system transfer function or from the input signal. This is the first part of a very concise and quite detailed explanation of the z-transform and not recommended for those dealing with the z-transform for the. Z-Transform; Z-Transform - Introduction; Z-Transform - Properties; Z-Transform - Existence; Z-Transform - Inverse; Z-Transform - Solved Examples; Discrete Fourier Transform; DFT - Introduction; DFT - Time Frequency Transform; DTF - Circular Convolution; DFT - Linear Filtering; DFT - Sectional Convolution; DFT - Discrete Cosine Transform; DFT. Table 3: Properties of the z-Transform Property Sequence Transform ROC xn X(z) R x1n X1(z) R1 x2n X2(z) R2 Linearity ax1n+bx2n aX1(z)+bX2(z) At least the intersection of R1 and R2 Time shifting xn −n0 z−n0X(z) R except for the possible addition or deletion of the origin Scaling in the ejω0nxn X(e−jω0z) R z-Domain zn 0xn.
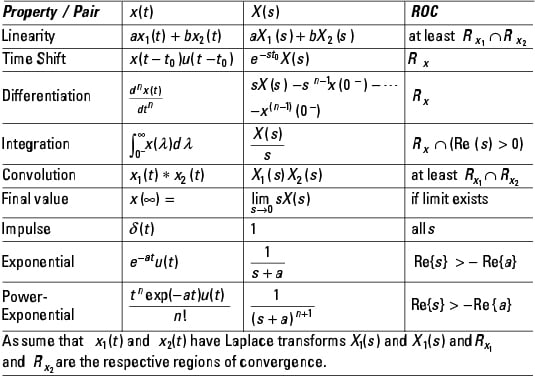
| Entry | Laplace Domain | Time Domain (Note) All time domain functions are implicitly=0 for t<0 (i.e. they are multiplied by unit step). | Z Domain (t=kT) |
|---|---|---|---|
| unit impulse | unit impulse | ||
| unit step | (Note) u(t) is more commonly used to represent the step function, but u(t) is also used to represent other things. We choose gamma (γ(t)) to avoid confusion (and because in the Laplace domain (Γ(s)) it looks a little like a step input). | ||
| ramp | |||
| parabola | |||
| tn (n is integer) | |||
| exponential | |||
| power | |||
| time multiplied exponential | |||
| Asymptotic exponential | |||
| double exponential | |||
| asymptotic double exponential | |||
| asymptotic critically damped | |||
| differentiated critically damped | |||
| sine | |||
| cosine | |||
| decaying sine | |||
| decaying cosine | |||
| generic decaying oscillatory | |||
| generic decaying oscillatory (alternate) | (Note) atan is the arctangent (tan-1) function. The atan function can give incorrect results (typically the function is written so that the result is always in quadrants I or IV). To ensure accuracy, use a function that corrects for this. In most programming languages the function is atan2. Also be careful about using degrees and radians as appropriate. | ||
| Z-domain generic decaying oscillatory | (Note) | ||
| Prototype Second Order System (ζ<1, underdampded) | |||
| Prototype 2nd order lowpass step response | |||
| Prototype 2nd order lowpass impulse response | |||
| Prototype 2nd order bandpass impulse response | |||
Using this table for Z Transforms with discrete indices
Commonly the 'time domain' function is given in terms of a discrete index, k, rather than time. This is easily accommodated by the table. For example if you are given a function:
Since t=kT, simply replace k in the function definition by k=t/T. So, in this case,

Z Transform Pairs
and we can use the table entry for the ramp
The answer is then easily obtained
z-Transform
Sometimes one has the problem to make two samples comparable, i.e. to compare measured values of a sample with respect to their (relative) position in the distribution. An often used aid is the z-transform which converts the values of a sample into z-scores:
with
zi ... z-transformed sample observations
xi ... original values of the sample
... sample mean
s ... standard deviation of the sample
Z Transform Table E^at
The z-transform is also called standardization or auto-scaling. z-Scores become comparable by measuring the observations in multiples of the standard deviation of that sample. The mean of a z-transformed sample is always zero. If the original distribution is a normal one, the z-transformed data belong to a standard normal distribution (μ=0, s=1).
The following example demonstrates the effect of the standardization of the data. Assume we have two normal distributions, one with mean of 10.0 and a standard deviation of 30.0 (top left), the other with a mean of 200 and a standard deviation of 20.0 (top right). The standardization of both data sets results in comparable distributions since both z-transformed distributions have a mean of 0.0 and a standard deviation of 1.0 (bottom row).
Inverse Z Transform Matlab
| Hint: | In some published papers you can read that the z-scores are normally distributed. This is wrong - the z-transform does not change the form of the distribution, it only adjusts the mean and the standard deviation. Pictorially speaking, the distribution is simply shifted along the x axis and expanded or compressed to achieve a zero mean and standard deviation of 1.0. |